Graphs Theory and Geography
Graphs Theory and Geography
PeterBurbery
Analyzing countries in Europe, Africa, and Asia as nodes or vertices in a graph that are connected if they border each other. I use different centrality measures to measure closeness, betweenness, the Katz centrality, eigenvector centrality, and eccentricity.
Vertex Eccentricity
Vertex Eccentricity
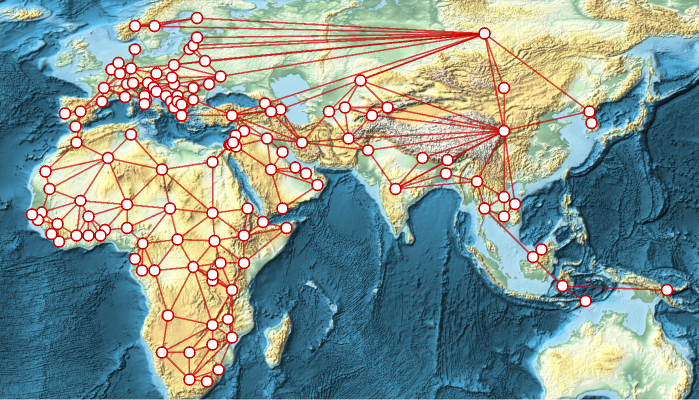
Make a graph of countries in Eurasia and Africa with tooltips with the name and flag of the country when you hover over a place.
ℰ=UndirectedGraph@NestGraph#["BorderingCountries"]&,,12;GeoGraphPlotℰ,ImageSize->Full,
Out[]=
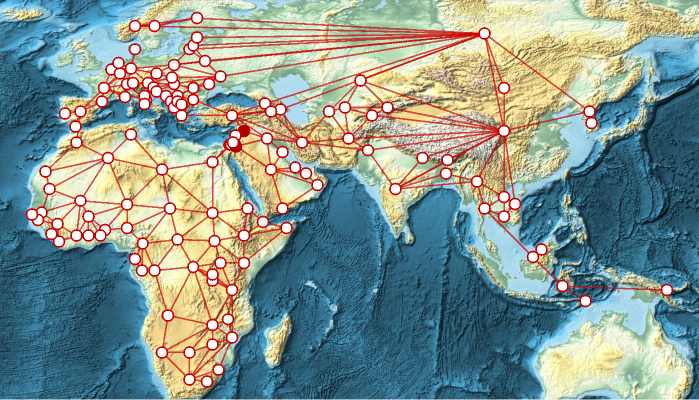
Which countries are closest to the ? This is the graph center:
Highlight the graph center in the graph:
GeoGraphPlotℰ,ImageSize->Full,
Out[]=
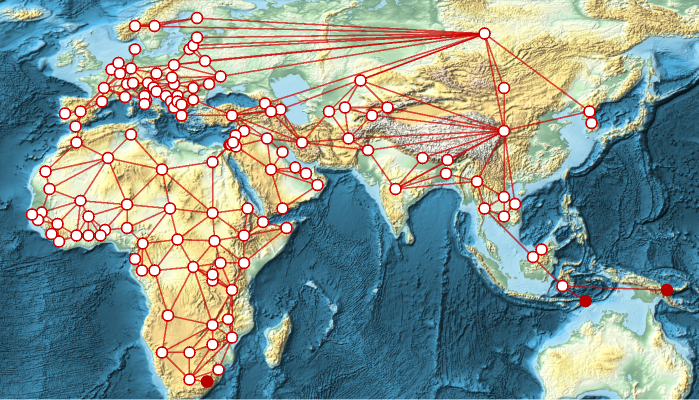
The graph periphery is the farthest part of the graph. This helps us find the most distant countries:
GeoGraphPlotℰ,ImageSize->Full,
Out[]=
We can compute the distance to travel from Lesotho, East Timor, and Papua New Guinea with GraphDiameter and the same quantity for Jordan and Syria with Graph Radius:
In[]:=
GraphRadius[ℰ]
Out[]=
9
In[]:=
GraphDiameter[ℰ]
Out[]=
18
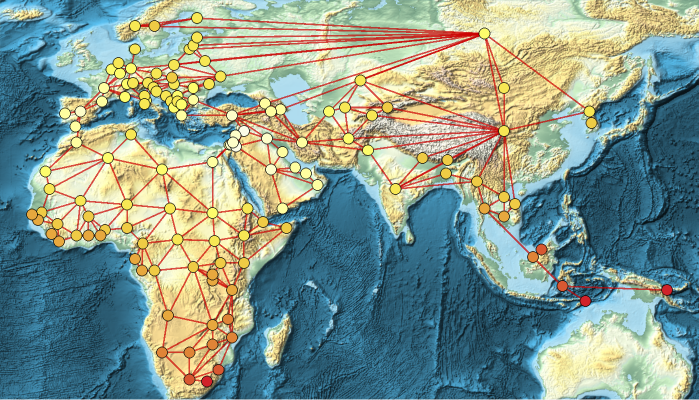
Study the vertex eccentricity of countries:
In[]:=
EurasiaCountries=VertexList[ℰ];EurasiavertexEccentricity=AssociationMap[VertexEccentricity[ℰ,#]&,EurasiaCountries];ReverseSort[EurasiavertexEccentricity]//Short
Out[]//Short=
18,18,18,17,17,17,17,16,16,16,16,16,16,15,15,15,15,100,11,11,11,11,11,11,11,11,10,10,10,10,10,10,10,9,9
Add vertex highlighting based on the vertex :
GeoGraphPlotℰ,ImageSize->Full,
Out[]=
Let' s analyze countries based on the number of other countries they border, or in the case of graph theory, the degree of each country's vertex:
Find the country with the highest vertex degree, which is the graph hub:
Analyze the degree centrality:
Closeness Centrality
Closeness Centrality
Closeness centrality gives high centralities to vertices that are at a short average distance to every other reachable vertex. The closer a country is to other countries the more important the country.
Find the countries that can most efficiently communicate with every other organization and that can facilitate the quick spread of viruses such as COVID:
The countries with large closeness centrality can spread things easily, such as immigration, ideas, computer viruses, and goods. Closeness is the reciprocal of farness. The closeness metric helps locate countries critical to global supply chain network and essential to Internet communication.
Betweenness Centrality
Betweenness Centrality
Betweenness measures the number of shortest paths a country is on. High betweenness means disruptions are much more devastating because the shortest path is no longer possible if the node with many shortest path is stopped:
The countries with large betweenness are critical and if a disruption happens the path between two countries will be affected.
Rank countries by their importance in preventing disruptions in the flow of people and goods and trade:
Eigenvector Centrality
Eigenvector Centrality
Eigenvector centrality measures how well-connected vertices are to other well-connected vertices. The more important countries should have more resources invested by businesses for maximum connection with other well-connected countries.
Find the eigenvector centrality:
Katz Centrality
Katz Centrality
See countries who can efficiently spread culture:
Predict a partition of the countries in case of a conflict between influential members :
I want to highlight similar to the example for HighlightGraph and KatzCentrality with the Zachary Karate Club but I can't figure it out.